นางสาวโยธญา อิศรเสนา ณอยุธยา ม.6/1 เลขที่ 30

อัตราการเปลี่ยนแปลง

ถ้าเรามีกราฟแสดงการเจริญเติบโตของต้นไม้ เป็นกราฟที่บอกความสูงของต้นไม้ ณ เวลาต่างๆ ต้นไม้หนึ่งต้นมีความสูงค่าเดียว ณ เวลาหนึ่งๆ ความสูงของต้นไม้จึงเป็นฟังก์ชัน มีอินพุตเป็นเวลา และให้ค่าความสูงออกมาเมื่อวาดกราฟฟังก์ชันความสูงของต้นไม้ จิ้มจุดมาสองจุดบนเส้นโค้งของกราฟ แล้วลากเส้นตรงเชื่อมระหว่างกัน เราจะได้เส้นเอียงๆ (หรืออาจจะไม่เอียงก็ได้) มาเส้นหนึ่ง ความชันของเส้นตรงเส้นนั้นเรียกว่าอัตราการเจริญเติบโตของต้นไม้ เพราะได้จากการเอาค่าของ “การเจริญเติบโต” (ความสูงที่เพิ่มขึ้น) หารด้วยเวลาที่เปลี่ยนไปการหาอัตราการเปลี่ยนแปลงของปริมาณอย่างอื่นๆนอกเหนือจากการเติบโตของต้นไม้ ถ้าใช้เรขาคณิตเป็นเครื่องมือ เราจะต้องมีจุดสองจุดที่อยู่บนกราฟของฟังก์ชัน ลากเส้นเชื่อมเข้าด้วยกันเพื่อหาความชัน แล้วความชันของเส้นนั้นจะคืออัตราการเปลี่ยนแปลงเฉลี่ย

http://www.tewlek.com/anet_cal.html

อัตราการเปลี่ยนแปลง

ถ้าเรามีกราฟแสดงการเจริญเติบโตของต้นไม้ เป็นกราฟที่บอกความสูงของต้นไม้ ณ เวลาต่างๆ ต้นไม้หนึ่งต้นมีความสูงค่าเดียว ณ เวลาหนึ่งๆ ความสูงของต้นไม้จึงเป็นฟังก์ชัน มีอินพุตเป็นเวลา และให้ค่าความสูงออกมา

เมื่อวาดกราฟฟังก์ชันความสูงของต้นไม้ จิ้มจุดมาสองจุดบนเส้นโค้งของกราฟ แล้วลากเส้นตรงเชื่อมระหว่างกัน เราจะได้เส้นเอียงๆ (หรืออาจจะไม่เอียงก็ได้) มาเส้นหนึ่ง ความชันของเส้นตรงเส้นนั้นเรียกว่าอัตราการเจริญเติบโตของต้นไม้ เพราะได้จากการเอาค่าของ “การเจริญเติบโต” (ความสูงที่เพิ่มขึ้น) หารด้วยเวลาที่เปลี่ยนไป

การหาอัตราการเปลี่ยนแปลงของปริมาณอย่างอื่นๆนอกเหนือจากการเติบโตของต้นไม้ ถ้าใช้เรขาคณิตเป็นเครื่องมือ เราจะต้องมีจุดสองจุดที่อยู่บนกราฟของฟังก์ชัน ลากเส้นเชื่อมเข้าด้วยกันเพื่อหาความชัน แล้วความชันของเส้นนั้นจะคืออัตราการเปลี่ยนแปลงเฉลี่ย

Name  :  นายกฤษณวรรธน์  อุ่นเรือน ชั้นม.6/2  เลขที่ 1

Link    :  http://www.tewlek.com/anet_cal.html

 นางสาวผณินทร ผิวภูเขียว เลขที่ 23 ม. 6/1 

อนุพันธ์ (derivative) คือการหาค่าความเปลี่ยนแปลงของตัวแปรหนึ่ง
เมื่ออีกตัวแปรหนึ่งเปลี่ยนแปลงในปริมาณที่น้อยมากๆ
บางทีอนุพันธ์ที่เราจะได้พบครั้งแรกในโรงเรียนคือ สูตรอัตราเร็ว = ระยะทาง/เวลา สำหรับวัตถุที่เคลื่อนที่ด้วยอัตราเร็วคงที่
อัตราเร็วของคุณซึ่งเป็นอนุพันธ์ที่บอกการเปลี่ยนแปลงตำแหน่งในระยะเวลาหนึ่ง
วิชาแคลคูลัสพัฒนาขึ้น เพื่อจัดการกับปัญหาที่ซับซ้อนและเป็นธรรมชาติกว่านี้
ซึ่งอัตราเร็วของคุณอาจเปลี่ยนแปลงได้

เมื่อเรากล่าวถึงรายละเอียดแล้ว
แคลคูลัสเชิงอนุพันธ์ นิยามอัตราการเปลี่ยนแปลงในขณะใดขณะหนึ่ง (อนุพันธ์) ระหว่างค่าของฟังก์ชัน กับตัวแปรของฟังก์ชัน นิยามจริงๆ ของอนุพันธ์คือ ลิมิตของอัตราส่วนในการเปลี่ยนแปลง (difference
quotient). อนุพันธ์คือหัวใจของวิทยาศาสตร์กายภาพ กฎการเคลื่อนที่ของนิวตัน แรง = มวล×ความเร่ง มีความหมายในแคลคูลัส
เพราะว่า ความเร่งเป็นอนุพันธ์ค่าหนึ่ง ทฤษฎีแม่เหล็กไฟฟ้าของแมกซ์เวล และทฤษฎีแรงโน้มถ่วงของไอน์สไตน์ (สัมพัทธภาพทั่วไป)
นั่นได้กล่าวถึงด้วยภาษาของแคลคูลัสเชิงอนุพันธ์ เช่นเดียวกันกับทฤษฎีพื้นฐานของวงจรไฟฟ้า

อนุพันธ์ของฟังก์ชัน
กล่าวถึงกราฟของฟังก์ชันนั้นในช่วงสั้น ๆ ซึ่งทำให้เราสามารถหาจุดสูงสุด
และจุดต่ำสุด ของฟังก์ชันได้ เพราะว่าที่จุดเหล่านั้นกราฟจะขนานกับแกนราบ
ดิเฟอเรนเชียล แคลคูลัสยังมีการประยุกต์ใช้อื่นๆอีก เช่น ระเบียบวิธีของนิวตัน (Newton's
Method) ซึ่งเป็นวิธีในการหาค่ารากของฟังก์ชัน โดยการประมาณค่าโดยเส้นสัมผัส
ดังนั้นแคลคูลัสเชิงอนุพันธ์ จึง

สามารถนำไปประยุกต์ใช้กับหลากหลายคำถาม
ซึ่งถ้ามองแค่ผิวเผินอาจคิดว่า ไม่อาจใช้แคลคูลัสจัดการได้

http://www.learners.in.th/blogs/posts/354020

นางสาวปาจรีย์  คงหาญ  เลขที่ 33 ม.6/1

อัตราการเปลี่ยนแปลง

ถ้าเรามีกราฟแสดงการเจริญเติบโตของต้นไม้ เป็นกราฟที่บอกความสูงของต้นไม้ ณ เวลาต่างๆ ต้นไม้หนึ่งต้นมีความสูงค่าเดียว ณ เวลาหนึ่งๆ ความสูงของต้นไม้จึงเป็นฟังก์ชัน มีอินพุตเป็นเวลา และให้ค่าความสูงออกมา

เมื่อวาดกราฟฟังก์ชันความสูงของต้นไม้ จิ้มจุดมาสองจุดบนเส้นโค้งของกราฟ แล้วลากเส้นตรงเชื่อมระหว่างกัน เราจะได้เส้นเอียงๆ (หรืออาจจะไม่เอียงก็ได้) มาเส้นหนึ่ง ความชันของเส้นตรงเส้นนั้นเรียกว่าอัตราการเจริญเติบโตของต้นไม้ เพราะได้จากการเอาค่าของ “การเจริญเติบโต” (ความสูงที่เพิ่มขึ้น) หารด้วยเวลาที่เปลี่ยนไป

การหาอัตราการเปลี่ยนแปลงของปริมาณอย่างอื่นๆนอกเหนือจากการเติบโตของต้นไม้ ถ้าใช้เรขาคณิตเป็นเครื่องมือ เราจะต้องมีจุดสองจุดที่อยู่บนกราฟของฟังก์ชัน ลากเส้นเชื่อมเข้าด้วยกันเพื่อหาความชัน แล้วความชันของเส้นนั้นจะคืออัตราการเปลี่ยนแปลงเฉลี่ย

ถ้าเมื่อไหร่เกิดอยากหาอัตราการเปลี่ยนแปลงขณะหนึ่ง คือลงไปดูที่เวลาค่าใดค่าหนึ่งเป๊ะๆ ไม่เอาค่าเฉลี่ยบนช่วงเวลา เราจะเกิดปัญหากับเรขาคณิตทันที เพราะมีเวลาและค่าของฟังก์ชันแค่จุดเดียว ยังไงก็ไม่สามารถหาอัตราการเปลี่ยนแปลงได้ ถ้าจะเข้าสูตรความชันของเส้นตรงก็จะมีปัญหาว่า “ตัวหารเป็นศูนย์”

ถึงตรงนี้ลิมิตเข้ามาช่วยเราไว้ ในเรื่องลิมิตเราพูดได้ว่า “จุดเดียว” นั้นคือลิมิตของการที่สองจุดเคลื่อนเข้ามาใกล้กัน ความชันของกราฟที่จุดจุดเดียว ถึงเรขาคณิตจะหาไม่ได้ แต่เรานิยามให้มันคือลิมิตของความชันระหว่างสองจุดรอบๆบริเวณที่เราต้องการได้

เมื่อมีสองจุดในตอนแรกก็หาความชันกราฟได้ปกติ เมื่อสองจุดค่อยๆเคลื่อนเข้ามาหากัน ความชันกราฟก็จะเป็นค่าที่คำนวณบนช่วงเล็กลงเรื่อยๆ จนเมื่อสองจุดทับกัน ความชันก็จะหายไปเพราะไม่สามารถคำนวณตรงๆได้ แต่เราจะนิยามมันขึ้นมาให้เท่ากับค่าลิมิตของความชันที่คำนวณจากช่วงแคบๆรอบๆจุดนั้น พร้อมกับตั้งชื่อให้มันใหม่ว่า “อนุพันธ์”

ผลพลอยได้จากการทำแบบนี้ก็คือ เราได้เส้นสัมผัสกราฟที่จุด x จากเดิมที่การวัดความชันต้องสร้าง 2 จุดที่อยู่ห่างกันแล้วลากเส้นตรงเชื่อมสองจุดนั้น ถ้ากราฟเป็นเส้นโค้ง ความชันกับเส้นกราฟจะตัดกัน (ไม่สัมผัสกัน) แต่เมื่อลากสองจุดให้มาอยู่ติดกัน จุดที่คำนวณความชันของกราฟจะแตะกับเส้นสัมผัสพอดี ความชันของกราฟ ณ ตำแหน่งนั้น จะเท่ากับความชันของเส้นสัมผัสกราฟ และมีค่าเท่ากับอนุพันธ์ที่เรากำลังคำนวณอยู่

ตอนนี้เรามีหลายคำที่ความหมายเหมือนกัน ได้แก่ ความชันของกราฟ ณ จุดจุดหนึ่ง, ความชันของเส้นสัมผัสกราฟ, อนุพันธ์, และอัตราการเปลี่ยนแปลงขณะหนึ่ง … คำว่าความชันเป็นความหมายในเชิงเรขาคณิต ส่วนอัตราการเปลี่ยนแปลงนั้นเป็นคำทั่วๆไป คำว่าอนุพันธ์เป็นชื่อที่หมายถึงสิ่งเหล่านี้ทั้งหมด ซึ่งใช้เวลาที่ยุ่งเกี่ยวกับฟังก์ชัน จะได้ไม่ต้องเรียกด้วยคำยาวๆ

http://fltsolver.wordpress.com/tag

 น.ส อินทุอร สุนทร ม.6/1 เลขที่ 24

แคลคูลัส เป็นสาขาหลักของคณิตศาสตร์ซึ่งพัฒนามาจากพีชคณิต เราขาคณิต และปัญหาทางฟิสิกส์ แคลคูลัสมีต้นกำเนิดจากสองแนวคิดหลัก ดังนี้
แนวคิดแรกคือ แคลคูลัสเชิงอนุพันธ์ (Differential Calculus) เป็นทฤษฎีที่ว่าด้วยอัตราการเปลี่ยนแปลง และเกี่ยวข้องกับการหาอนุพันธ์ของฟังก์ชั่นทางคณิตศาสตร์ ตัวอย่างเช่น การหา ความเร็ว, ความเร่ง หรือความชันของเส้นโค้ง บนจุดที่กำหนดให้. ทฤษฎีของอนุพันธ์หลายส่วนได้แรงบันดาลใจจากปัญหาทางฟิสิกส์
แนวคิดที่สองคือ แคลคูลัสเชิงปริพันธ์ (Integral Calculus) เป็นทฤษฎีที่ได้แรงบันดาลใจจากการคำนวณหาพื้นที่หรือปริมาตรของรูปทรงทางเรขาคณิตต่าง ๆ. ทฤษฎีนี้ใช้กราฟของฟังก์ชันแทนรูปทรงทางเรขาคณิต และใช้ทฤษฎีปริพันธ์ (หรืออินทิเกรด) เป็นหลักในการคำนวณหาพื้นที่และปริมาตร
ทั้งสองแนวคิดที่กำเนิดจากปัญหาที่ต่างกันกลับมีความสัมพันธ์กันลึกซึ้ง โดยทฤษฎีบทมูลฐานของแคลคูลัสกล่าวว่า แท้จริงแล้วทฤษฎีทั้งสองเปรียบเสมือนเป็นด้านทั้งสองของเหรียญอันเดียวกัน นั่นคือเป็นสิ่งเดียวกันเพียงแต่มองคนละมุมเท่านั้น (โดยคร่าว ๆ เรากล่าวได้ว่าอนุพันธ์และปริพันธ์เป็นฟังก์ชั่นผูกพันของกันและกัน). ในการสอนแคลคูลัสเพื่อความเข้าใจตัวทฤษฎีอย่างลึกซึ้ง ควรกล่าวถึงทั้งสองทฤษฎีและความสัมพันธ์นี้ก่อน แต่การศึกษาในปัจจุบันมักจะกล่าวถึงแคลคูลัสเชิงอนุพันธ์ก่อนเพียงอย่างเดียว เนื่องจากนำไปใช้งานได้ง่ายกว่า
อนึ่ง การศึกษาแคลคูลัสอย่างละเอียดในเวลาต่อมา ได้ทำให้เกิดศาสตร์ใหม่ ๆ ทางคณิตศาสตร์มากมาย เช่น คณิตวิเคราะห์ และ ทฤษฎีการวัด เป็นต้น
แคลคูลัสเชิงอนุพันธ์
      อนุพันธ์ (derivative) คือการหาค่าความเปลี่ยนแปลงของตัวแปรหนึ่ง เมื่ออีกตัวแปรหนึ่งเปลี่ยนแปลงในปริมาณที่น้อยมากๆ บางทีอนุพันธ์ที่เราจะได้พบครั้งแรกในโรงเรียนคือ สูตร อัตราเร็ว = ระยะทาง/เวลาสำหรับวัตถุที่เคลื่อนที่ด้วยอัตราเร็วคงที่ อัตราเร็วของคุณซึ่งเป็นอนุพันธ์ที่บอกการเปลี่ยนแปลงตำแหน่งในระยะเวลาหนึ่ง วิชาแคลคูลัสพัฒนาขึ้น เพื่อจัดการกับปัญหาที่ซับซ้อนและเป็นธรรมชาติกว่านี้ ซึ่งอัตราเร็วของคุณอาจเปลี่ยนแปลงได้
      เมื่อเรากล่าวถึงรายละเอียดแล้ว แคลคูลัสเชิงอนุพันธ์ นิยามอัตราการเปลี่ยนแปลงในขณะใดขณะหนึ่ง (อนุพันธ์) ระหว่างค่าของฟังก์ชั่น กับตัวแปรของฟังก์ชัน นิยามจริงๆ ของอนุพันธ์คือ ลิมิตของอัตราส่วนในการเปลี่ยนแปลง (difference quotient). อนุพันธ์คือหัวใจของวิทยาศาสตร์กายภาพ กฎการเคลื่อนที่ของนิวตัน แรง = มวล×ความเร่ง มีความหมายในแคลคูลัส เพราะว่า ความเร่งเป็นอนุพันธ์ค่าหนึ่ง ทฤษฎีแม่เหล็กไฟฟ้าของแมกซ์เวล และทฤษฎีแรงโน้มถ่วงของไอน์สไตน์ (สัมพัทธภาพทั่วไป) นั่นได้กล่าวถึงด้วยภาษาของแคลคูลัสเชิงอนุพันธ์ เช่นเดียวกันกับทฤษฎีพื้นฐานของวงจรไฟฟ้า
       อนุพันธ์ของฟังก์ชัน กล่าวถึงกราฟของฟังก์ชันนั้นในช่วงสั้น ๆ ซึ่งทำให้เราสามารถหาจุดสูงสุด และจุดต่ำสุด ของฟังก์ชันได้ เพราะว่าที่จุดเหล่านั้นกราฟจะขนานกับแกนราบ ดิเฟอเรนเชียล แคลคูลัสยังมีการประยุกต์ใช้อื่นๆอีก เช่น ระเบียบวิธีของนิวตัน (Newton's Method) ซึ่งเป็นวิธีในการหาค่ารากของฟังก์ชัน โดยการประมาณค่าโดยเส้นสัมผัส ดังนั้นแคลคูลัสเชิงอนุพันธ์ จึงสามารถนำไปประยุกต์ใช้กับหลากหลายคำถาม ซึ่งถ้ามองแค่ผิวเผินอาจคิดว่า ไม่อาจใช้แคลคูลัสจัดการได้
แคลคูลัสเชิงปริพันธ์
      แคลคูลัสเชิงปริพันธ์ศึกษาวิธีการหาปริพันธ์ (อินทิกรัล, Integral) ของฟังก์ชัน ซึ่งอาจนิยามจากลิมิตของผลรวมของพจน์ (ซึ่งเรียกว่าลิมิตของผลรวมรีมันน์) แต่ละพจน์นั้นคือพื้นที่ที่เป็นสี่เหลี่ยมผืนผ้าแต่ละแถบใต้กราฟของฟังก์ชัน ทำให้การอินทิเกรตเป็นวิธีที่ได้ผลวิธีหนึ่งในการหาพื้นที่ใต้กราฟ และพื้นที่ผิว และปริมาตรของแข็งเช่นทรงกลมและทรงกระบอกพื้นฐานของแคลคูลัส

      
      
      พื้นฐานที่เคร่งครัดของแคลคูลัส มีฐานมาจาก แนวคิดของฟังก์ชั่น และลิมิต มันรวมเทคนิคของพีชคณิตพื้นฐาน และการอุปนัยเชิงคณิตศาสตร์ การศึกษาพื้นฐานของแคลคูลัสสมัยใหม่ รู้จักกันในชื่อ การวิเคราะห์เชิงจริง ซึ่งประกอบด้วย นิยามที่เคร่งครัด และบทพิสูจน์ของทฤษฎีของแคลคูลัส เช่นทฤษฎีการวัด และการวิเคราะห์เชิงฟังก์ชั่นทฤษฎีบทมูลฐานของแคลคูลัส เบื้องต้น

      
      
      ทฤษฎีบทมูลฐานของแคลคูลัสกล่าวว่า การหาอนุพันธ์และการหาปริพันธ์เป็นวิธีการที่ตรงกันข้ามกัน กล่าวคือ ถ้าเราสร้างฟังก์ชันที่เป็นปริพันธ์ของฟังก์ชันหนึ่งขี้นมา อนุพันธ์ของฟังก์ชันที่เราสร้าง ก็จะเท่ากับฟังก์ชันนั้น นอกจากนี้ เรายังหาปริพันธ์จำกัดเขตได้ด้วยการกำหนดค่าให้กับปฏิยานุพันธ์
      ทฤษฎีบทมูลฐานของแคลคูลัสเขียนในรูปสัญลักษณ์คณิตศาสตร์ได้ดังนี้: ถ้า f เป็นฟังก์ชันที่มีความต่อเนื่องบนช่วง [a, b] และ F เป็นปฏิยานุพันธ์ของ f บนช่วง [a, b] แล้ว

และสำหรับทุก x ในช่วง [a, b] จะได้ว่า

ความจริงข้อนี้ปรากฏแก่ทั้งนิวตัน และไลบ์นิซ ซึ่งเป็นกุญแจนำไปสู่ การขยายผลลัพธ์เชิงวิเคราะห์อย่างมากมายหลังจากงานของทั้งสองเป็นที่รู้จัก. ความเชื่อมโยงนี้ ทำให้เราสามารถย้อนความเปลี่ยนแปลงทั้งหมดในฟังก์ชันในช่วงหนึ่ง จากอัตราการเปลี่ยนแปลงในขณะใดขณะหนึ่ง โดยการหาปริพันธ์ของส่วนหลัง. ทฤษฎีบทมูลฐานนี้ยังให้วิธีในการคำนวณหา ปริพันธ์จำกัดเขต ด้วยวิธีทางพีชคณิตเป็นจำนวนมาก โดยไม่ต้องใช้วิธีการหาลิมิต ด้วยการหาปฎิยานุพันธ์ ทฤษฎีบทนี้ยังอนุญาตให้เราแก้สมการเชิงอนุพันธ์ ซึ่งคือสมการที่เกี่ยวข้องกันระหว่าง ฟังก์ชันที่ไม่ทราบค่า และอนุพันธ์ของมัน. สมการเชิงอนุพันธ์นั้นมีอยู่ทั่วไปในวิทยาศาสตร์
การประยุกต์นำมาใช้
     การพัฒนาและการใช้แคลคูลัสได้ขยายผลไปแทบทุกส่วนของการใช้ชีวิตในยุคใหม่ มันเป็นพื้นฐานของวิทยาศาสตร์เกือบทุกสาขาโดยเฉพาะ ฟิสิกส์ การพัฒนาสมัยใหม่เกือบทั้งหมด เช่น เทคนิคการก่อสร้าง การบิน และเทคโนโลยีอื่น ๆ เกือบทั้งหมด มีพื้นฐานมาจากแคลคูลัส
     แคลคูลัสได้ขยายไปสู่ สมการเชิงอนุพันธ์ แคลคูลัสเวกเตอร์ แคลคูลัสของการเปลี่ยนแปลง การวิเคราะห์เชิงซ้อน แคลคูลัสเชิงเวลา แคลคูลัสกณิกนันต์ และ ทอพอโลยีเชิงอนุพันธ์

แคลคูลัส(Calculus)

1.    ลิมิตของฟังก์ชัน  เขียนแทนด้วย    lim   f(x)  =  L

หมายถึง  x มีค่าเข้าใกล้ a  (x  a)  แล้ว  f(x) จะมีค่าเข้าใกล้ L

วิธีหา  ค่าลิมิตของฟังก์ชัน
(1).    เอาค่า a ไปแทนใน x ใน f(x) ถ้าผลที่ได้เป็นจำนวนจริงค่านั้นคือ ค่าลิมิต
(2).    เอาค่า a ไปแทนใน x ใน f(x)แล้วปรากฏผลออกมาในรูป
ให้พิจารณาลักษณะของฟังก์ชัน ดังนี้
(2.1)    ถ้าสามารถแยก f(x) ออกเป็นผลคูณของตัวประกอบได้ ก็ให้แยกแล้วขจัดตัวประกอบร่วมของเศษและส่วนออก หลังจากนั้นก็เอาค่า a ไปแทน x ถ้าผลที่ได้เป็นจำนวนจริง ค่านั้นคือค่าลิมิต
(2.2)    ถ้าแยกตัวประกอบไม่ได้ เนื่องจาก f(x) มักอยู่ในรูป
ก็ให้นำคอนจูเกตคูณทั้งเศษและส่วน  แล้วขจัดตัวประกอบที่ทำให้ส่วนเป็นศูนย์ออก  หลังจากนั้นก็เอาค่า a ไปแทน x ถ้าผลที่ได้เป็นจำนวนจริง ค่านั้นคือค่าลิมิต
2.  ความต่อเนื่องของฟังก์ชัน    ในทางคณิตศาสตร์ตรวจสอบว่า f จะต่อเนื่องที่
x = a หรือไม่นั้น  ต้องตรวจสอบจากคุณสมบัติ  3  ข้อต่อไปนี้
1.    หา f(a)  ได้
2.   lim f(x)   หาค่าได้

3.  lim f(x)  =  f(a)

3.  อัตราการเปลี่ยนแปลงโดยเฉลี่ย ของ y  หรือ f(x)  ในช่วง x1  ถึง x1+h   คือ
f(x1-h) - f(x1)
h

4. อัตราการเปลี่ยนแปลง ของ y = f(x) ณ x = x1

lim  f(x+h) - f(x)   คือ อัตราการเปลี่ยนแปลง ของ y = f(x) ณ x ใด ๆ
h

5.    อนุพันธ์ของฟังก์ชัน f   แทนด้วย  f /(x)  หรือ  dy/dx
ถ้า  y = f(x)   เป็นฟังก์ชันที่มีโดเมนและเรนจ์เป็นสับเซตของเซตจำนวนจริงเราเรียก lim         f(x+h) - f(x)   ที่หาได้ว่า อนุพันธ์ของฟังก์ชัน f ที่ x
h
6.    สูตรในการหาอนุพันธ์ของฟังก์ชัน
สูตรที่ 1.    ถ้า y = f(x) = c  เป็นค่าคงที่    dy/dx  = f/(x)  = 0
สูตรที่ 2.    ถ้า y = f(x) = x            dy/dx  = f/(x)  = 1
สูตรที่ 3.    ถ้า y = f(x) = xn  เมื่อ n เป็นจำนวนจริง    dy/dx  = f/(x)  =nxn-1
สูตรที่ 4.    ถ้า y = f(x) = g(x) + h(x)        dy/dx  = g/ (x) + h/ (x)
สูตรที่ 5.    ถ้า y = f(x) = g(x) - h(x)        dy/dx  = g/ (x) - h/ (x)
สูตรที่ 6.    ถ้า y = f(x) = cg(x)             dy/dx  = cg/ (x)
สูตรที่ 7.    ถ้า y = f(x) = g(x) h(x)        dy/dx  = g/(x)h(x)+h/ (x)g(x)
สูตรที่ 8.    ถ้า y = f(x) =     g(x)       เมื่อ h(x)  0
h(x)
dy/dx  = g/(x)h(x) - h/(x)g(x)
h(x)   2
สูตรที่ 9.    ถ้า y = f(x) = un  เมื่อ u เป็นฟังก์ชันของ x และ n เป็นจำนวนจริงจะได้ว่า    dy/dx  = nun-1 du/dx

ตัวอย่าง  ถ้า   f(x) = (x2 + 3x + 5)8    จงหาค่าของ dy/dx
วิธีทำ        dy/dx  =  8(x2 + 3x + 5)7  d (x2 + 3x + 5)
dx
=  8(x2 + 3x + 5)7(2x+3)
7.    วิธีหาค่าจุดสูงสุดสัมพัทธ์หรือจุดต่ำสุดสัมพัทธ์
7.1    หา  dy/dx  =  f/(x)
7.2    ให้ dy/dx  =  f/(x)  =  0
7.3    แก้สมการหาค่าตัวแปร  x  ที่จะทำให้ f(x)  มีค่าสูงสุดสัมพัทธ์หรือจุดต่ำสุดสัมพัทธ์  หรือไม่เกิดค่า 2 อย่างดังกล่าวก็ได้  เราเรียกค่า x นี้ว่า   ค่าวิกฤต
7.4    นำค่า x ดังกล่าวนี้มาตรวจสอบว่าทำให้ f(x) มีค่าสูงสุด หรือต่ำสุดสัมพัทธ์ หรือไม่เป็นทั้งสองอย่าง ซึ่งมีวิธีการตรวจสอบได้ 2 วิธีดังนี้
(1)    ตรวจสอบดูจากเครื่องหมายความชัน
ก.    ถ้าความชัน f/(x)  เปลี่ยนจากบวกเป็นลบ แสดงว่าจุดดังกล่าวเป็นจุดสูงสุดสัมพัทธ์
ข.    ถ้าความชัน f/(x)  เปลี่ยนจากลบเป็นบวก แสดงว่าจุดดังกล่าวเป็นจุดต่ำสุดสัมพัทธ์
ค.    ถ้าไม่เป็นไปตามข้อ ก  หรือ  ข  แสดงว่าจุดดังกล่าวไม่เป็นทั้งจุดสูงสุดและต่ำสุดสัมพัทธ์
(2)    ตรวจสอบดูจากเครื่องหมายของ  f//(x)
ก.  ถ้า f//(x) > 0   แสดงว่าเป็นจุดต่ำสุดสัมพัทธ์
ข.  ถ้า f//(x) < 0   แสดงว่าเป็นจุดสูงสุดสัมพัทธ์
ค.  ถ้า f//(x) = 0   แสดงว่าการตรวจสอบวิธีนี้ใช้ไม่ได้ ต้องย้อนกลับไปใช้วิธี(1)

8.    อินทิกรัลไม่จำกัดเขต    เรียกเครื่องหมาย           ว่า เครื่องหมายอิทิกรัล

สืบค้น ณ วันที่ 11/11/2555

http://www.google.co.th/url?sa=t&rct=j&q=&esrc=s&source=web&cd=31&cad=rj...

   นางสาวชาลิสา  ว่องวชิราพาณิชย์  ม.6/1  เลขที่ 6

“อัตราการเปลี่ยนแปลง”

อัตราการเปลี่ยนแปลงจะเกี่ยวข้องกับการหาอนุพันธ์ของฟังก์ชันทางคณิตศาสตร์

 ตัวอย่างเช่น การหา ความเร็ว, ความเร่ง หรือความชันของเส้นโค้ง บนจุดที่กำหนดให้

 ทฤษฎีของอนุพันธ์หลายส่วนได้แรงบันดาลใจจากปัญหาทางฟิสิกส์                                                             

            http://www.tewlek.com/anet_cal.html

นางสาวกมลทิพย์  น้อยรักษ์  ม6/1  เลขที่ 29

   อนุพันธ์ (derivative) คือการหาค่าความเปลี่ยนแปลงของตัวแปรหนึ่ง
เมื่ออีกตัวแปรหนึ่งเปลี่ยนแปลงในปริมาณที่น้อยมากๆ
บางทีอนุพันธ์ที่เราจะได้พบครั้งแรกในโรงเรียนคือ สูตรอัตราเร็ว = ระยะทาง/เวลา สำหรับวัตถุที่เคลื่อนที่ด้วยอัตราเร็วคงที่
อัตราเร็วของคุณซึ่งเป็นอนุพันธ์ที่บอกการเปลี่ยนแปลงตำแหน่งในระยะเวลาหนึ่ง
วิชาแคลคูลัสพัฒนาขึ้น เพื่อจัดการกับปัญหาที่ซับซ้อนและเป็นธรรมชาติกว่านี้
ซึ่งอัตราเร็วของคุณอาจเปลี่ยนแปลงได้

          เมื่อเรากล่าวถึงรายละเอียดแล้ว
แคลคูลัสเชิงอนุพันธ์ นิยามอัตราการเปลี่ยนแปลงในขณะใดขณะหนึ่ง (อนุพันธ์) ระหว่างค่าของฟังก์ชัน กับตัวแปรของฟังก์ชัน นิยามจริงๆ ของอนุพันธ์คือ ลิมิตของอัตราส่วนในการเปลี่ยนแปลง (difference
quotient). อนุพันธ์คือหัวใจของวิทยาศาสตร์กายภาพ กฎการเคลื่อนที่ของนิวตัน แรง = มวล×ความเร่ง มีความหมายในแคลคูลัส
เพราะว่า ความเร่งเป็นอนุพันธ์ค่าหนึ่ง ทฤษฎีแม่เหล็กไฟฟ้าของแมกซ์เวล และทฤษฎีแรงโน้มถ่วงของไอน์สไตน์ (สัมพัทธภาพทั่วไป)
นั่นได้กล่าวถึงด้วยภาษาของแคลคูลัสเชิงอนุพันธ์ เช่นเดียวกันกับทฤษฎีพื้นฐานของวงจรไฟฟ้า

           อนุพันธ์ของฟังก์ชัน
กล่าวถึงกราฟของฟังก์ชันนั้นในช่วงสั้น ๆ ซึ่งทำให้เราสามารถหาจุดสูงสุด
และจุดต่ำสุด ของฟังก์ชันได้ เพราะว่าที่จุดเหล่านั้นกราฟจะขนานกับแกนราบ
ดิเฟอเรนเชียล แคลคูลัสยังมีการประยุกต์ใช้อื่นๆอีก เช่น ระเบียบวิธีของนิวตัน (Newton's
Method) ซึ่งเป็นวิธีในการหาค่ารากของฟังก์ชัน โดยการประมาณค่าโดยเส้นสัมผัส
ดังนั้นแคลคูลัสเชิงอนุพันธ์ จึง

สามารถนำไปประยุกต์ใช้กับหลากหลายคำถาม
ซึ่งถ้ามองแค่ผิวเผินอาจคิดว่า ไม่อาจใช้แคลคูลัสจัดการได้

http://www.learners.in.th/blogs/posts/354020

http://th.wikipedia.org/wiki/%E0%B9%81%E0%B8%84%E0%B8%A5%E0%B8%84%E0%B8%B9%E0%B8%A5%E0%B8%B1%E0%B8%AA#.E0.B8.81.E0.B8.B2.E0.B8.A3.E0.B8.9B.E0.B8.A3.E0.B8.B0.E0.B8.A2.E0.B8.B8.E0.B8.81.E0.B8.95.E0.B9.8C.E0.B8.99.E0.B8.B3.E0.B8.A1.E0.B8.B2.E0.B9.83.E0.B8.8A.E0.B9.89 

นาสาวจิตรา   เส็งสี   เลขที่ 8 ชั้นม. 6/1

แคลคูลัสเชิงอนุพันธ์

เมื่อเรากล่าวถึงรายละเอียดแล้ว แคลคูลัสเชิงอนุพันธ์ นิยามอัตราการเปลี่ยนแปลงในขณะใดขณะหนึ่ง (อนุพันธ์) ระหว่างค่าของฟังก์ชัน กับตัวแปรของฟังก์ชัน นิยามจริงๆ ของอนุพันธ์คือ ลิมิตของอัตราส่วนในการเปลี่ยนแปลง (difference quotient). อนุพันธ์คือหัวใจของวิทยาศาสตร์กายภาพ กฎการเคลื่อนที่ของนิวตัน แรง = มวล×ความเร่ง มีความหมายในแคลคูลัส เพราะว่า ความเร่งเป็นอนุพันธ์ค่าหนึ่ง ทฤษฎีแม่เหล็กไฟฟ้าของแมกซ์เวลและทฤษฎีแรงโน้มถ่วงของไอน์สไตน์ (สัมพัทธภาพทั่วไป) นั่นได้กล่าวถึงด้วยภาษาของแคลคูลัสเชิงอนุพันธ์ เช่นเดียวกันกับทฤษฎีพื้นฐานของวงจรไฟฟ้า

อนุพันธ์ของฟังก์ชัน กล่าวถึงกราฟของฟังก์ชันนั้นในช่วงสั้น ๆ ซึ่งทำให้เราสามารถหาจุดสูงสุด และจุดต่ำสุด ของฟังก์ชันได้ เพราะว่าที่จุดเหล่านั้นกราฟจะขนานกับแกนราบ ดิเฟอเรนเชียล แคลคูลัสยังมีการประยุกต์ใช้อื่นๆอีก เช่น ระเบียบวิธีของนิวตัน (Newton's Method) ซึ่งเป็นวิธีในการหาค่ารากของฟังก์ชัน โดยการประมาณค่าโดยเส้นสัมผัส ดังนั้นแคลคูลัสเชิงอนุพันธ์ จึงสามารถนำไปประยุกต์ใช้กับหลากหลายคำถาม ซึ่งถ้ามองแค่ผิวเผินอาจคิดว่า ไม่อาจใช้แคลคูลัสจัดการได้

สูตรการหาอนุพันธ์ 

[แก้]

นางสาวนัจนันท์ ทองสวัสดิื ม.6/2 เลขที่12  ปล.อ.ค่ะของหนูเข้าไม่ได้เลยใช้ของเพื่อนส่งก่อนนะคะ

 อัตราการเปลี่ยนแปลงที่ “จุดเดียว”

ถ้าเรามีกราฟแสดงการเจริญเติบโตของต้นไม้ เป็นกราฟที่บอกความสูงของต้นไม้ ณ เวลาต่างๆ ต้นไม้หนึ่งต้นมีความสูงค่าเดียว ณ เวลาหนึ่งๆ ความสูงของต้นไม้จึงเป็นฟังก์ชัน มีอินพุตเป็นเวลา และให้ค่าความสูงออกมา

เมื่อวาดกราฟฟังก์ชันความสูงของต้นไม้ จิ้มจุดมาสองจุดบนเส้นโค้งของกราฟ แล้วลากเส้นตรงเชื่อมระหว่างกัน เราจะได้เส้นเอียงๆ (หรืออาจจะไม่เอียงก็ได้) มาเส้นหนึ่ง ความชันของเส้นตรงเส้นนั้นเรียกว่าอัตราการเจริญเติบโตของต้นไม้ เพราะได้จากการเอาค่าของ “การเจริญเติบโต” (ความสูงที่เพิ่มขึ้น) หารด้วยเวลาที่เปลี่ยนไป

การหาอัตราการเปลี่ยนแปลงของปริมาณอย่างอื่นๆนอกเหนือจากการเติบโตของต้นไม้ ถ้าใช้เรขาคณิตเป็นเครื่องมือ เราจะต้องมีจุดสองจุดที่อยู่บนกราฟของฟังก์ชัน ลากเส้นเชื่อมเข้าด้วยกันเพื่อหาความชัน แล้วความชันของเส้นนั้นจะคืออัตราการเปลี่ยนแปลงเฉลี่ย

ถ้าเมื่อไหร่เกิดอยากหาอัตราการเปลี่ยนแปลงขณะหนึ่ง คือลงไปดูที่เวลาค่าใดค่าหนึ่งเป๊ะๆ ไม่เอาค่าเฉลี่ยบนช่วงเวลา เราจะเกิดปัญหากับเรขาคณิตทันที เพราะมีเวลาและค่าของฟังก์ชันแค่จุดเดียว ยังไงก็ไม่สามารถหาอัตราการเปลี่ยนแปลงได้ ถ้าจะเข้าสูตรความชันของเส้นตรงก็จะมีปัญหาว่า “ตัวหารเป็นศูนย์”

ถึงตรงนี้ลิมิตเข้ามาช่วยเราไว้ ในเรื่องลิมิตเราพูดได้ว่า “จุดเดียว” นั้นคือลิมิตของการที่สองจุดเคลื่อนเข้ามาใกล้กัน ความชันของกราฟที่จุดจุดเดียว ถึงเรขาคณิตจะหาไม่ได้ แต่เรานิยามให้มันคือลิมิตของความชันระหว่างสองจุดรอบๆบริเวณที่เราต้องการได้

เมื่อมีสองจุดในตอนแรกก็หาความชันกราฟได้ปกติ เมื่อสองจุดค่อยๆเคลื่อนเข้ามาหากัน ความชันกราฟก็จะเป็นค่าที่คำนวณบนช่วงเล็กลงเรื่อยๆ จนเมื่อสองจุดทับกัน ความชันก็จะหายไปเพราะไม่สามารถคำนวณตรงๆได้ แต่เราจะนิยามมันขึ้นมาให้เท่ากับค่าลิมิตของความชันที่คำนวณจากช่วงแคบๆรอบๆจุดนั้น พร้อมกับตั้งชื่อให้มันใหม่ว่า “อนุพันธ์”

ผลพลอยได้จากการทำแบบนี้ก็คือ เราได้เส้นสัมผัสกราฟที่จุด x จากเดิมที่การวัดความชันต้องสร้าง 2 จุดที่อยู่ห่างกันแล้วลากเส้นตรงเชื่อมสองจุดนั้น ถ้ากราฟเป็นเส้นโค้ง ความชันกับเส้นกราฟจะตัดกัน (ไม่สัมผัสกัน) แต่เมื่อลากสองจุดให้มาอยู่ติดกัน จุดที่คำนวณความชันของกราฟจะแตะกับเส้นสัมผัสพอดี ความชันของกราฟ ณ ตำแหน่งนั้น จะเท่ากับความชันของเส้นสัมผัสกราฟ และมีค่าเท่ากับอนุพันธ์ที่เรากำลังคำนวณอยู่

ตอนนี้เรามีหลายคำที่ความหมายเหมือนกัน ได้แก่ ความชันของกราฟ ณ จุดจุดหนึ่ง, ความชันของเส้นสัมผัสกราฟ, อนุพันธ์, และอัตราการเปลี่ยนแปลงขณะหนึ่ง … คำว่าความชันเป็นความหมายในเชิงเรขาคณิต ส่วนอัตราการเปลี่ยนแปลงนั้นเป็นคำทั่วๆไป คำว่าอนุพันธ์เป็นชื่อที่หมายถึงสิ่งเหล่านี้ทั้งหมด ซึ่งใช้เวลาที่ยุ่งเกี่ยวกับฟังก์ชัน จะได้ไม่ต้องเรียกด้วยคำยาวๆ

 http://fltsolver.wordpress.com/tag/%E0%B8%AD%E0%B8%B1%E0%B8%95%E0%B8%A3%E0%B8%B2%E0%B8%81%E0%B8%B2%E0%B8%A3%E0%B9%80%E0%B8%9B%E0%B8%A5%E0%B8%B5%E0%B9%88%E0%B8%A2%E0%B8%99%E0%B9%81%E0%B8%9B%E0%B8%A5%E0%B8%87/

นางสาว เกษรินทร์  เนื่องชมภู  เลขที่ 24  ชั้นม.6/2

 http://www.google.co.th/search?num=10&hl=th&site=imghp&tbm=isch&source=hp&biw=1366&bih=667&q=%E0%B9%80%E0%B9%80%E0%B8%84%E0%B8%A7%E0%B8%94%E0%B8%B9%E0%B8%A5%E0%B8%B1%E0%B8%AA&oq=%E0%B9%80%E0%B9%80%E0%B8%84%E0%B8%A7%E0%B8%94%E0%B8%B9%E0%B8%A5%E0%B8%B1%E0%B8%AA&gs_l=img.3...8338.22067.0.22335.15.8.1.6.0.0.809.3587.1j1j4-2j3j1.8.0...0.0...1ac.1.cNRbpd0d-9s

นางสาว วนิดา  เหมือนจิตร เลขที่ 15  ชั้นม.6/2

 http://www.google.co.th/search?num=10&hl=th&site=imghp&tbm=isch&source=hp&biw=1366&bih=667&q=แคลคูลัส&oq=แคลดู&gs_l=img.3.0.0i10i24.596.7193.0.9441.7.6.1.0.0.0.673.2596.1j0j1j0j1j3.6.0...0.0.

นางสาว เกษรินทร์ เนื่องชมภู เลชที่ 24   ชั้นมัธยมศึกษาปีที่ 6/2 

แคลคูลัส เป็นสาขาหลักของคณิตศาสตร์ซึ่งพัฒนามาจากพีชคณิต เรขาคณิต และปัญหาทางฟิสิกส์ แคลคูลัสมีต้นกำเนิดจากสองแนวคิดหลัก ดังนี้

แนวคิดแรกคือ แคลคูลัสเชิงอนุพันธ์ (Differential Calculus) เป็นทฤษฎีที่ว่าด้วยอัตราการเปลี่ยนแปลง และเกี่ยวข้องกับการหาอนุพันธ์ของฟังก์ชันทางคณิตศาสตร์ ตัวอย่างเช่น การหา ความเร็ว, ความเร่ง หรือความชันของเส้นโค้ง บนจุดที่กำหนดให้. ทฤษฎีของอนุพันธ์หลายส่วนได้แรงบันดาลใจจากปัญหาทางฟิสิกส์

แนวคิดที่สองคือ แคลคูลัสเชิงปริพันธ์ (Integral Calculus) เป็นทฤษฎีที่ได้แรงบันดาลใจจากการคำนวณหาพื้นที่หรือปริมาตรของรูปทรงทางเรขาคณิตต่าง ๆ. ทฤษฎีนี้ใช้กราฟของฟังก์ชันแทนรูปทรงทางเรขาคณิต และใช้ทฤษฎีปริพันธ์ (หรืออินทิเกรต) เป็นหลักในการคำนวณหาพื้นที่และปริมาตร

ทั้งสองแนวคิดที่กำเนิดจากปัญหาที่ต่างกันกลับมีความสัมพันธ์กันลึกซึ้ง โดยทฤษฎีบทมูลฐานของแคลคูลัสกล่าวว่า แท้จริงแล้วทฤษฎีทั้งสองเปรียบเสมือนเป็นด้านทั้งสองของเหรียญอันเดียวกัน นั่นคือเป็นสิ่งเดียวกันเพียงแต่มองคนละมุมเท่านั้น (โดยคร่าว ๆ เรากล่าวได้ว่าอนุพันธ์และปริพันธ์เป็นฟังก์ชันผกผันของกันและกัน). ในการสอนแคลคูลัสเพื่อความเข้าใจตัวทฤษฎีอย่างลึกซึ้ง ควรกล่าวถึงทั้งสองทฤษฎีและความสัมพันธ์นี้ก่อน แต่การศึกษาในปัจจุบันมักจะกล่าวถึงแคลคูลัสเชิงอนุพันธ์ก่อนเพียงอย่างเดียว เนื่องจากนำไปใช้งานได้ง่ายกว่า

อนึ่ง การศึกษาแคลคูลัสอย่างละเอียดในเวลาต่อมา ได้ทำให้เกิดศาสตร์ใหม่ ๆ ทางคณิตศาสตร์มากมาย เช่น คณิตวิเคราะห์ และ ทฤษฎีการวัด เป็นต้น

 ส่งใหม่ครับ พรชัย คำเชิด ม.6/2 เลขที่ 6

นิยามอัตราการเปลี่ยนแปลง

ในฟังก์ชัน
 y = f(x)
ใดๆ เราพิจารณา อัตราการเปลี่ยนแปลงของค่าฟังก์ชัน ได้ดังนี้

ที่จุด
x =  x₁                     จะได้  y = f(x₁)

ที่จุด x =  x₂ =  x₁ + h           จะได้   y = f(x₁ + h)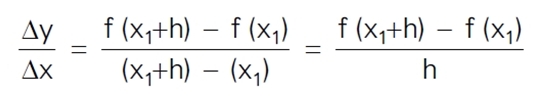
ดังนั้น
อัตราการเปลี่ยนแปลงเฉลี่ยของ y เทียบกับ x ในช่วง x₁
ถึง x₁ + h
ก็คือ

  อัตราการเปลี่ยนแปลงโดยเฉลี่ยของ  y เทียบกับ
x (ในช่วง x ถึง x + h ใดๆ) คือ

หรือ

 และเมื่อเราบีบช่วง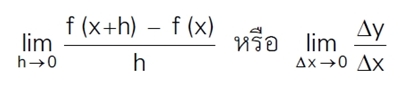
h ให้แคบลงจนถึงใกล้
0 ก็จะได้อัตราการเปลี่ยนแปลง ณ จุด x ที่กำหนด ฉะนั้น อัตราการเปลี่ยนแปลงโดยเฉลี่ยของ
 y (ที่จุด X ใดๆ) คือ

 (ไม่สามารถแทนค่า
h = 0
ลงไปตรงๆได้ เพราะจะเป็น 0/0 จึงต้องใช้ลิมิตในการช่วยคำนวณ)

 ตัวอย่าง
ถ้า y = f(x) = 2x²+3x-4

ให้หาอัตราการเปลี่ยนแปลงของ
y เทียบกับ
x

ก.
โดยเฉลี่ยช่วง x=1 ถึง 4

วิธีคิด

 (แปลว่าในช่วงที่กำหนดนี้
เมื่อ x เพื่มขึ้น 1 หน่วยแล้ว y จะเพิ่มขึ้นประมาณ 13
หน่วย)

 ข.
ที่จุดซึ่ง x=2

 (คำนวณโดยติดค่า
x ใดๆ
ไว้ก่อน จนได้ผลเป็น 4x+3 แล้วจึงแทนค่า x=2 ลงไปได้)

นายพงษธร  อยู่สุข  ม.6/2  เลขที่ 5

อัตราการเปลี่ยนแปลงที่ “จุดเดียว”

ถ้าเรามีกราฟแสดงการเจริญเติบโตของต้นไม้ เป็นกราฟที่บอกความสูงของต้นไม้ ณ เวลาต่างๆ ต้นไม้หนึ่งต้นมีความสูงค่าเดียว ณ เวลาหนึ่งๆ ความสูงของต้นไม้จึงเป็นฟังก์ชัน มีอินพุตเป็นเวลา และให้ค่าความสูงออกมา

เมื่อวาดกราฟฟังก์ชันความสูงของต้นไม้ จิ้มจุดมาสองจุดบนเส้นโค้งของกราฟ แล้วลากเส้นตรงเชื่อมระหว่างกัน เราจะได้เส้นเอียงๆ (หรืออาจจะไม่เอียงก็ได้) มาเส้นหนึ่ง ความชันของเส้นตรงเส้นนั้นเรียกว่าอัตราการเจริญเติบโตของต้นไม้ เพราะได้จากการเอาค่าของ “การเจริญเติบโต” (ความสูงที่เพิ่มขึ้น) หารด้วยเวลาที่เปลี่ยนไป

การหาอัตราการเปลี่ยนแปลงของปริมาณอย่างอื่นๆนอกเหนือจากการเติบโตของต้นไม้ ถ้าใช้เรขาคณิตเป็นเครื่องมือ เราจะต้องมีจุดสองจุดที่อยู่บนกราฟของฟังก์ชัน ลากเส้นเชื่อมเข้าด้วยกันเพื่อหาความชัน แล้วความชันของเส้นนั้นจะคืออัตราการเปลี่ยนแปลงเฉลี่ย

ถ้าเมื่อไหร่เกิดอยากหาอัตราการเปลี่ยนแปลงขณะหนึ่ง คือลงไปดูที่เวลาค่าใดค่าหนึ่งเป๊ะๆ ไม่เอาค่าเฉลี่ยบนช่วงเวลา เราจะเกิดปัญหากับเรขาคณิตทันที เพราะมีเวลาและค่าของฟังก์ชันแค่จุดเดียว ยังไงก็ไม่สามารถหาอัตราการเปลี่ยนแปลงได้ ถ้าจะเข้าสูตรความชันของเส้นตรงก็จะมีปัญหาว่า “ตัวหารเป็นศูนย์”

ถึงตรงนี้ลิมิตเข้ามาช่วยเราไว้ ในเรื่องลิมิตเราพูดได้ว่า “จุดเดียว” นั้นคือลิมิตของการที่สองจุดเคลื่อนเข้ามาใกล้กัน ความชันของกราฟที่จุดจุดเดียว ถึงเรขาคณิตจะหาไม่ได้ แต่เรานิยามให้มันคือลิมิตของความชันระหว่างสองจุดรอบๆบริเวณที่เราต้องการได้

เมื่อมีสองจุดในตอนแรกก็หาความชันกราฟได้ปกติ เมื่อสองจุดค่อยๆเคลื่อนเข้ามาหากัน ความชันกราฟก็จะเป็นค่าที่คำนวณบนช่วงเล็กลงเรื่อยๆ จนเมื่อสองจุดทับกัน ความชันก็จะหายไปเพราะไม่สามารถคำนวณตรงๆได้ แต่เราจะนิยามมันขึ้นมาให้เท่ากับค่าลิมิตของความชันที่คำนวณจากช่วงแคบๆรอบๆจุดนั้น พร้อมกับตั้งชื่อให้มันใหม่ว่า “อนุพันธ์”

ผลพลอยได้จากการทำแบบนี้ก็คือ เราได้เส้นสัมผัสกราฟที่จุด x จากเดิมที่การวัดความชันต้องสร้าง 2 จุดที่อยู่ห่างกันแล้วลากเส้นตรงเชื่อมสองจุดนั้น ถ้ากราฟเป็นเส้นโค้ง ความชันกับเส้นกราฟจะตัดกัน (ไม่สัมผัสกัน) แต่เมื่อลากสองจุดให้มาอยู่ติดกัน จุดที่คำนวณความชันของกราฟจะแตะกับเส้นสัมผัสพอดี ความชันของกราฟ ณ ตำแหน่งนั้น จะเท่ากับความชันของเส้นสัมผัสกราฟ และมีค่าเท่ากับอนุพันธ์ที่เรากำลังคำนวณอยู่

ตอนนี้เรามีหลายคำที่ความหมายเหมือนกัน ได้แก่ ความชันของกราฟ ณ จุดจุดหนึ่ง, ความชันของเส้นสัมผัสกราฟ, อนุพันธ์, และอัตราการเปลี่ยนแปลงขณะหนึ่ง … คำว่าความชันเป็นความหมายในเชิงเรขาคณิต ส่วนอัตราการเปลี่ยนแปลงนั้นเป็นคำทั่วๆไป คำว่าอนุพันธ์เป็นชื่อที่หมายถึงสิ่งเหล่านี้ทั้งหมด ซึ่งใช้เวลาที่ยุ่งเกี่ยวกับฟังก์ชัน จะได้ไม่ต้องเรียกด้วยคำยาวๆ

http://fltsolver.wordpress.com/2011/11/14/%E0%B9%81%E0%B8%84%E0%B8%A5%E0%B8%84%E0%B8%B9%E0%B8%A5%E0%B8%B1%E0%B8%AA-%E0%B8%95%E0%B8%AD%E0%B8%99%E0%B8%97%E0%B8%B5%E0%B9%88-2/

นายอัครพงษ์ อินพึ่ง ม.6/1 เลขที่ 17

โรงเรียนนทบุรีพิทยาคม

แคลคูลัสเชิงอนุพันธ์

อนุพันธ์ (derivative) คือการหาค่าความเปลี่ยนแปลงของตัวแปรหนึ่ง เมื่ออีกตัวแปรหนึ่งเปลี่ยนแปลงในปริมาณที่น้อยมากๆ บางทีอนุพันธ์ที่เราจะได้พบครั้งแรกในโรงเรียนคือ สูตร อัตราเร็ว = ระยะทาง/เวลา สำหรับวัตถุที่เคลื่อนที่ด้วยอัตราเร็วคงที่ อัตราเร็วของคุณซึ่งเป็นอนุพันธ์ที่บอกการเปลี่ยนแปลงตำแหน่งในระยะเวลาหนึ่ง วิชาแคลคูลัสพัฒนาขึ้น เพื่อจัดการกับปัญหาที่ซับซ้อนและเป็นธรรมชาติกว่านี้ ซึ่งอัตราเร็วของคุณอาจเปลี่ยนแปลงได้

เมื่อเรากล่าวถึงรายละเอียดแล้ว แคลคูลัสเชิงอนุพันธ์ นิยามอัตราการเปลี่ยนแปลงในขณะใดขณะหนึ่ง (อนุพันธ์) ระหว่างค่าของฟังก์ชัน กับตัวแปรของฟังก์ชัน นิยามจริงๆ ของอนุพันธ์คือ ลิมิตของอัตราส่วนในการเปลี่ยนแปลง (difference quotient). อนุพันธ์คือหัวใจของวิทยาศาสตร์กายภาพ กฎการเคลื่อนที่ของนิวตัน แรง = มวล×ความเร่ง มีความหมายในแคลคูลัส เพราะว่า ความเร่งเป็นอนุพันธ์ค่าหนึ่ง ทฤษฎีแม่เหล็กไฟฟ้าของแมกซ์เวล และทฤษฎีแรงโน้มถ่วงของไอน์สไตน์ (สัมพัทธภาพทั่วไป) นั่นได้กล่าวถึงด้วยภาษาของแคลคูลัสเชิงอนุพันธ์ เช่นเดียวกันกับทฤษฎีพื้นฐานของวงจรไฟฟ้า

อนุพันธ์ของฟังก์ชัน กล่าวถึงกราฟของฟังก์ชันนั้นในช่วงสั้น ๆ ซึ่งทำให้เราสามารถหาจุดสูงสุด และจุดต่ำสุด ของฟังก์ชันได้ เพราะว่าที่จุดเหล่านั้นกราฟจะขนานกับแกนราบ ดิเฟอเรนเชียล แคลคูลัสยังมีการประยุกต์ใช้อื่นๆอีก เช่น ระเบียบวิธีของนิวตัน (Newton's Method) ซึ่งเป็นวิธีในการหาค่ารากของฟังก์ชัน โดยการประมาณค่าโดยเส้นสัมผัส ดังนั้นแคลคูลัสเชิงอนุพันธ์ จึงสามารถนำไปประยุกต์ใช้กับหลากหลายคำถาม ซึ่งถ้ามองแค่ผิวเผินอาจคิดว่า ไม่อาจใช้แคลคูลัสจัดการได้

นส  วนิดา เหมือนจิตร ม.6/2

นางสาวสุวรรณี  เวชสิทธิ์ ม.6/2 เลขที่ 9

แคลคูลัส เป็นสาขาหลักของคณิตศาสตร์ซึ่งพัฒนามาจากพีชคณิต เราขาคณิต และปัญหาทางฟิสิกส์ แคลคูลัสมีต้นกำเนิดจากสองแนวคิดหลัก ดังนี้

     แนวคิดแรกคือ แคลคูลัสเชิงอนุพันธ์ (Differential Calculus) เป็นทฤษฎีที่ว่าด้วยอัตราการเปลี่ยนแปลง และเกี่ยวข้องกับการหาอนุพันธ์ของฟังก์ชั่นทางคณิตศาสตร์ ตัวอย่างเช่น การหา ความเร็ว, ความเร่ง หรือความชันของเส้นโค้ง บนจุดที่กำหนดให้. ทฤษฎีของอนุพันธ์หลายส่วนได้แรงบันดาลใจจากปัญหาทางฟิสิกส์

     แนวคิดที่สองคือ แคลคูลัสเชิงปริพันธ์ (Integral Calculus) เป็นทฤษฎีที่ได้แรงบันดาลใจจากการคำนวณหาพื้นที่หรือปริมาตรของรูปทรงทางเรขาคณิตต่าง ๆ. ทฤษฎีนี้ใช้กราฟของฟังก์ชันแทนรูปทรงทางเรขาคณิต และใช้ทฤษฎีปริพันธ์ (หรืออินทิเกรด) เป็นหลักในการคำนวณหาพื้นที่และปริมาตร

     ทั้งสองแนวคิดที่กำเนิดจากปัญหาที่ต่างกันกลับมีความสัมพันธ์กันลึกซึ้ง โดยทฤษฎีบทมูลฐานของแคลคูลัสกล่าวว่า แท้จริงแล้วทฤษฎีทั้งสองเปรียบเสมือนเป็นด้านทั้งสองของเหรียญอันเดียวกัน นั่นคือเป็นสิ่งเดียวกันเพียงแต่มองคนละมุมเท่านั้น (โดยคร่าว ๆ เรากล่าวได้ว่าอนุพันธ์และปริพันธ์เป็นฟังก์ชั่นผูกพันของกันและกัน). ในการสอนแคลคูลัสเพื่อความเข้าใจตัวทฤษฎีอย่างลึกซึ้ง ควรกล่าวถึงทั้งสองทฤษฎีและความสัมพันธ์นี้ก่อน แต่การศึกษาในปัจจุบันมักจะกล่าวถึงแคลคูลัสเชิงอนุพันธ์ก่อนเพียงอย่างเดียว เนื่องจากนำไปใช้งานได้ง่ายกว่า
      อนึ่ง การศึกษาแคลคูลัสอย่างละเอียดในเวลาต่อมา ได้ทำให้เกิดศาสตร์ใหม่ ๆ ทางคณิตศาสตร์มากมาย เช่น คณิตวิเคราะห์ และ ทฤษฎีการวัด เป็นต้น

แคลคูลัสเชิงอนุพันธ์
      อนุพันธ์ (derivative) คือการหาค่าความเปลี่ยนแปลงของตัวแปรหนึ่ง เมื่ออีกตัวแปรหนึ่งเปลี่ยนแปลงในปริมาณที่น้อยมากๆ บางทีอนุพันธ์ที่เราจะได้พบครั้งแรกในโรงเรียนคือ สูตร อัตราเร็ว = ระยะทาง/เวลา สำหรับวัตถุที่เคลื่อนที่ด้วยอัตราเร็วคงที่ อัตราเร็วของคุณซึ่งเป็นอนุพันธ์ที่บอกการเปลี่ยนแปลงตำแหน่งในระยะเวลาหนึ่ง วิชาแคลคูลัสพัฒนาขึ้น เพื่อจัดการกับปัญหาที่ซับซ้อนและเป็นธรรมชาติกว่านี้ ซึ่งอัตราเร็วของคุณอาจเปลี่ยนแปลงได้
      เมื่อเรากล่าวถึงรายละเอียดแล้ว แคลคูลัสเชิงอนุพันธ์ นิยามอัตราการเปลี่ยนแปลงในขณะใดขณะหนึ่ง (อนุพันธ์) ระหว่างค่าของฟังก์ชั่น กับตัวแปรของฟังก์ชัน นิยามจริงๆ ของอนุพันธ์คือ ลิมิตของอัตราส่วนในการเปลี่ยนแปลง (difference quotient). อนุพันธ์คือหัวใจของวิทยาศาสตร์กายภาพ กฎการเคลื่อนที่ของนิวตัน แรง = มวล×ความเร่ง มีความหมายในแคลคูลัส เพราะว่า ความเร่งเป็นอนุพันธ์ค่าหนึ่ง ทฤษฎีแม่เหล็กไฟฟ้าของแมกซ์เวล และทฤษฎีแรงโน้มถ่วงของไอน์สไตน์ (สัมพัทธภาพทั่วไป) นั่นได้กล่าวถึงด้วยภาษาของแคลคูลัสเชิงอนุพันธ์ เช่นเดียวกันกับทฤษฎีพื้นฐานของวงจรไฟฟ้า
       อนุพันธ์ของฟังก์ชัน กล่าวถึงกราฟของฟังก์ชันนั้นในช่วงสั้น ๆ ซึ่งทำให้เราสามารถหาจุดสูงสุด และจุดต่ำสุด ของฟังก์ชันได้ เพราะว่าที่จุดเหล่านั้นกราฟจะขนานกับแกนราบ ดิเฟอเรนเชียล แคลคูลัสยังมีการประยุกต์ใช้อื่นๆอีก เช่น ระเบียบวิธีของนิวตัน (Newton's Method) ซึ่งเป็นวิธีในการหาค่ารากของฟังก์ชัน โดยการประมาณค่าโดยเส้นสัมผัส ดังนั้นแคลคูลัสเชิงอนุพันธ์ จึงสามารถนำไปประยุกต์ใช้กับหลากหลายคำถาม ซึ่งถ้ามองแค่ผิวเผินอาจคิดว่า ไม่อาจใช้แคลคูลัสจัดการได้

แคลคูลัสเชิงปริพันธ์
      แคลคูลัสเชิงปริพันธ์ศึกษาวิธีการหาปริพันธ์ (อินทิกรัล, Integral) ของฟังก์ชัน ซึ่งอาจนิยามจากลิมิตของผลรวมของพจน์ (ซึ่งเรียกว่าลิมิตของผลรวมรีมันน์) แต่ละพจน์นั้นคือพื้นที่ที่เป็นสี่เหลี่ยมผืนผ้าแต่ละแถบใต้กราฟของฟังก์ชัน ทำให้การอินทิเกรตเป็นวิธีที่ได้ผลวิธีหนึ่งในการหาพื้นที่ใต้กราฟ และพื้นที่ผิว และปริมาตรของแข็งเช่นทรงกลมและทรงกระบอกพื้นฐานของแคลคูลัส
      พื้นฐานที่เคร่งครัดของแคลคูลัส มีฐานมาจาก แนวคิดของฟังก์ชั่น และลิมิต มันรวมเทคนิคของพีชคณิตพื้นฐาน และการอุปนัยเชิงคณิตศาสตร์ การศึกษาพื้นฐานของแคลคูลัสสมัยใหม่ รู้จักกันในชื่อ การวิเคราะห์เชิงจริง ซึ่งประกอบด้วย นิยามที่เคร่งครัด และบทพิสูจน์ของทฤษฎีของแคลคูลัส เช่นทฤษฎีการวัด และการวิเคราะห์เชิงฟังก์ชั่นทฤษฎีบทมูลฐานของแคลคูลัส เบื้องต้น
      ทฤษฎีบทมูลฐานของแคลคูลัสกล่าวว่า การหาอนุพันธ์และการหาปริพันธ์เป็นวิธีการที่ตรงกันข้ามกัน กล่าวคือ ถ้าเราสร้างฟังก์ชันที่เป็นปริพันธ์ของฟังก์ชันหนึ่งขี้นมา อนุพันธ์ของฟังก์ชันที่เราสร้าง ก็จะเท่ากับฟังก์ชันนั้น นอกจากนี้ เรายังหาปริพันธ์จำกัดเขตได้ด้วยการกำหนดค่าให้กับปฏิยานุพันธ์

      ทฤษฎีบทมูลฐานของแคลคูลัสเขียนในรูปสัญลักษณ์คณิตศาสตร์ได้ดังนี้: ถ้า f เป็นฟังก์ชันที่มีความต่อเนื่องบนช่วง [a, b] และ F เป็นปฏิยานุพันธ์ของ f บนช่วง [a, b] แล้ว

และสำหรับทุก x ในช่วง [a, b] จะได้ว่า

        ความจริงข้อนี้ปรากฏแก่ทั้งนิวตัน และไลบ์นิซ ซึ่งเป็นกุญแจนำไปสู่ การขยายผลลัพธ์เชิงวิเคราะห์อย่างมากมายหลังจากงานของทั้งสองเป็นที่รู้จัก. ความเชื่อมโยงนี้ ทำให้เราสามารถย้อนความเปลี่ยนแปลงทั้งหมดในฟังก์ชันในช่วงหนึ่ง จากอัตราการเปลี่ยนแปลงในขณะใดขณะหนึ่ง โดยการหาปริพันธ์ของส่วนหลัง. ทฤษฎีบทมูลฐานนี้ยังให้วิธีในการคำนวณหา ปริพันธ์จำกัดเขต ด้วยวิธีทางพีชคณิตเป็นจำนวนมาก โดยไม่ต้องใช้วิธีการหาลิมิต ด้วยการหาปฎิยานุพันธ์ ทฤษฎีบทนี้ยังอนุญาตให้เราแก้สมการเชิงอนุพันธ์ ซึ่งคือสมการที่เกี่ยวข้องกันระหว่าง ฟังก์ชันที่ไม่ทราบค่า และอนุพันธ์ของมัน. สมการเชิงอนุพันธ์นั้นมีอยู่ทั่วไปในวิทยาศาสตร์

การประยุกต์นำมาใช้
     การพัฒนาและการใช้แคลคูลัสได้ขยายผลไปแทบทุกส่วนของการใช้ชีวิตในยุคใหม่ มันเป็นพื้นฐานของวิทยาศาสตร์เกือบทุกสาขาโดยเฉพาะ ฟิสิกส์ การพัฒนาสมัยใหม่เกือบทั้งหมด เช่น เทคนิคการก่อสร้าง การบิน และเทคโนโลยีอื่น ๆ เกือบทั้งหมด มีพื้นฐานมาจากแคลคูลัส
     แคลคูลัสได้ขยายไปสู่ สมการเชิงอนุพันธ์ แคลคูลัสเวกเตอร์ แคลคูลัสของการเปลี่ยนแปลง การวิเคราะห์เชิงซ้อน แคลคูลัสเชิงเวลา แคลคูลัสกณิกนันต์ และ ทอพอโลยีเชิงอนุพันธ์

แหล่งที่มา http://guru.sanook.com/pedia/topic/%E0%B9%81%E0%B8%84%E0%B8%A5%E0%B8%84%E0%B8%B9%E0%B8%A5%E0%B8%B1%E0%B8%AA/

นายสามารถศรีสุวรรณ ชั้น ม.6/2 เลขที่ 22
อัตราการเปลี่ยนแปลง
แคลคูลัส เป็นสาขาหลักของคณิตศาสตร์ซึ่งพัฒนามาจากพีชคณิต เรขาคณิต และปัญหาทางฟิสิกส์ แคลคูลัสมีต้นกำเนิดจากสองแนวคิดหลัก ดังนี้
แนวคิดแรกคือ แคลคูลัสเชิงอนุพันธ์ (Differential Calculus) เป็นทฤษฎีที่ว่าด้วยอัตราการเปลี่ยนแปลง และเกี่ยวข้องกับการหาอนุพันธ์ของฟังก์ชันทางคณิตศาสตร์ ตัวอย่างเช่น การหา ความเร็ว, ความเร่ง หรือความชันของเส้นโค้ง บนจุดที่กำหนดให้. ทฤษฎีของอนุพันธ์หลายส่วนได้แรงบันดาลใจจากปัญหาทางฟิสิกส์
แนวคิดที่สองคือ แคลคูลัสเชิงปริพันธ์ (Integral Calculus) เป็นทฤษฎีที่ได้แรงบันดาลใจจากการคำนวณหาพื้นที่หรือปริมาตรของรูปทรงทางเรขาคณิตต่าง ๆ. ทฤษฎีนี้ใช้กราฟของฟังก์ชันแทนรูปทรงทางเรขาคณิต และใช้ทฤษฎีปริพันธ์ (หรืออินทิเกรต) เป็นหลักในการคำนวณหาพื้นที่และปริมาตร
ทั้งสองแนวคิดที่กำเนิดจากปัญหาที่ต่างกันกลับมีความสัมพันธ์กันลึกซึ้ง โดยทฤษฎีบทมูลฐานของแคลคูลัสกล่าวว่า แท้จริงแล้วทฤษฎีทั้งสองเปรียบเสมือนเป็นด้านทั้งสองของเหรียญอันเดียวกัน นั่นคือเป็นสิ่งเดียวกันเพียงแต่มองคนละมุมเท่านั้น (โดยคร่าว ๆ เรากล่าวได้ว่าอนุพันธ์และปริพันธ์เป็นฟังก์ชันผกผันของกันและกัน). ในการสอนแคลคูลัสเพื่อความเข้าใจตัวทฤษฎีอย่างลึกซึ้ง ควรกล่าวถึงทั้งสองทฤษฎีและความสัมพันธ์นี้ก่อน แต่การศึกษาในปัจจุบันมักจะกล่าวถึงแคลคูลัสเชิงอนุพันธ์ก่อนเพียงอย่างเดียว เนื่องจากนำไปใช้งานได้ง่ายกว่า
อนึ่ง การศึกษาแคลคูลัสอย่างละเอียดในเวลาต่อมา ได้ทำให้เกิดศาสตร์ใหม่ ๆ ทางคณิตศาสตร์มากมาย เช่น คณิตวิเคราะห์ และ ทฤษฎีการวัด เป็นต้น

http://th.wikipedia.org/wiki/%E0%B9%81%E0%B8%84%E0%B8%A5%E0%B8%84%E0%B8%...

นายเทพนรินทร์ ผาสุขมูล ม.6/2 เลขที่ 27

โรงเรียนนนทบุรีพิทยาคม

แคลคูลัส เป็นสาขาหลักของคณิตศาสตร์ซึ่งพัฒนามาจากพีชคณิต เรขาคณิต และปัญหาทางฟิสิกส์ แคลคูลัสมีต้นกำเนิดจากสองแนวคิดหลัก ดังนี้

แนวคิดแรกคือ แคลคูลัสเชิงอนุพันธ์ (Differential Calculus) เป็นทฤษฎีที่ว่าด้วยอัตราการเปลี่ยนแปลง และเกี่ยวข้องกับการหาอนุพันธ์ของฟังก์ชันทางคณิตศาสตร์ ตัวอย่างเช่น การหา ความเร็ว, ความเร่ง หรือความชันของเส้นโค้ง บนจุดที่กำหนดให้. ทฤษฎีของอนุพันธ์หลายส่วนได้แรงบันดาลใจจากปัญหาทางฟิสิกส์

แนวคิดที่สองคือ แคลคูลัสเชิงปริพันธ์ (Integral Calculus) เป็นทฤษฎีที่ได้แรงบันดาลใจจากการคำนวณหาพื้นที่หรือปริมาตรของรูปทรงทางเรขาคณิตต่าง ๆ. ทฤษฎีนี้ใช้กราฟของฟังก์ชันแทนรูปทรงทางเรขาคณิต และใช้ทฤษฎีปริพันธ์ (หรืออินทิเกรต) เป็นหลักในการคำนวณหาพื้นที่และปริมาตร

ทั้งสองแนวคิดที่กำเนิดจากปัญหาที่ต่างกันกลับมีความสัมพันธ์กันลึกซึ้ง โดยทฤษฎีบทมูลฐานของแคลคูลัสกล่าวว่า แท้จริงแล้วทฤษฎีทั้งสองเปรียบเสมือนเป็นด้านทั้งสองของเหรียญอันเดียวกัน นั่นคือเป็นสิ่งเดียวกันเพียงแต่มองคนละมุมเท่านั้น (โดยคร่าว ๆ เรากล่าวได้ว่าอนุพันธ์และปริพันธ์เป็นฟังก์ชันผกผันของ
กันและกัน). ในการสอนแคลคูลัสเพื่อความเข้าใจตัวทฤษฎีอย่างลึกซึ้ง
ควรกล่าวถึงทั้งสองทฤษฎีและความสัมพันธ์นี้ก่อน
แต่การศึกษาในปัจจุบันมักจะกล่าวถึงแคลคูลัสเชิงอนุพันธ์ก่อนเพียงอย่าง
เดียว เนื่องจากนำไปใช้งานได้ง่ายกว่า

อนึ่ง การศึกษาแคลคูลัสอย่างละเอียดในเวลาต่อมา ได้ทำให้เกิดศาสตร์ใหม่ ๆ ทางคณิตศาสตร์มากมาย เช่น คณิตวิเคราะห์ และ ทฤษฎีการวัด เป็นต้น

http://th.wikipedia.org/wiki/%E0%B9%81%E0%B8%84%E0%B8%A5%E0%B8%84%E0%B8%...

น.ส.ชุลีพร ประพงศ์พันธ์ เลขที่ 11

ความเร็วเฉลี่ย

ขณะที่วัตถุมีการเคลื่อนที่ในแนวเส้นตรง เราจะเห็นว่าตาแหน่งของวัตถุเปลี่ยนไป ถ้า ทราบตาแหน่งเดิมของวัตถุและทราบตาแหน่งใหม่ของวัตถุที่เคลื่อนที่ไป เราจะทราบระยะห่าง จากตาแหน่งเดิมและทิศทางที่วัตถุเคลื่อนที่ อัตราส่วนของระยะห่างของวัตถุจากตาแหน่ง เดิม (โดยคิดทิศทาง) ต่อเวลาทั้งหมดที่ใช้ในการเคลื่อนที่จากตา แหน่งเดิมไปตา แหน่ง ใหม่ เรียกว่า ความเร็วเฉลี่ย ซึ่ งความเร็วเฉลี่ย แทนด้วยจานวนจริงจะเป็นจานวนจริงบวก หรือลบก็ได้ การเป็นบวกหรือลบจะแสดงทิศทางของการเคลื่อนที่ ถ้าให้ t เป็นเวลาที่วัตถุใช้ในการเคลื่อนที่ในแนวเส้นตรง มีหน่วยเป็นวินาที และ s เป็น ระยะทางที่วัดจากจุดเริ่มต้นเพื่อบอกตาแหน่งของวัตถุเมื่อเวลาผ่านไป t วินาที มีหน่วยเป็นเมตร จะเห็นได้ว่า ระยะทางที่วัตถุเคลื่อนที่ได้มีความสัมพันธ์กับเวลาที่ใช้ในการเคลื่อนที่ หรืออาจกล่าว ได้ว่า ระยะทางของการเคลื่อนที่ของวัตถุจะอยู่ในรูปของฟังก์ชันของเวลา ซึ่ งเขียนแทนด้วย s = f(t) เรียกสมการนี้ ว่า สมการการเคลื่อนที่

ดังนั้น ความเร็วเฉลี่ยในช่วงเวลาจาก t ถึง t + h เท่ากับ เมตรต่อวินาที h tf ht f ) () ( 

ความเร็วเฉลี่ยขณะเวลาt ใดๆเท่ากับเมตรต่อวินาh t f h t f h ) ( ) ( lim0   

พรชัย คำเชิด ม.6/2 เลขที่ 6

1. อัตราการเปลี่ยนแปลงโดยเฉลี่ย ของ y หรือ f(x) ในช่วง x1 ถึง x1+h คือ
f(x1-h) - f(x1)
h

2. อัตราการเปลี่ยนแปลง ของ y = f(x) ณ x = x1

lim f(x+h) - f(x) คือ อัตราการเปลี่ยนแปลง ของ y = f(x) ณ x ใด ๆ
h

3. อนุพันธ์ของฟังก์ชัน f แทนด้วย f /(x) หรือ dy/dx
ถ้า y = f(x) เป็นฟังก์ชันที่มีโดเมนและเรนจ์เป็นสับเซตของเซตจำนวนจริงเราเรียก lim f(x+h) - f(x) ที่หาได้ว่า อนุพันธ์ของฟังก์ชัน f ที่ x
h
4. สูตรในการหาอนุพันธ์ของฟังก์ชัน
สูตรที่ 1. ถ้า y = f(x) = c เป็นค่าคงที่ dy/dx = f/(x) = 0
สูตรที่ 2. ถ้า y = f(x) = x dy/dx = f/(x) = 1
สูตรที่ 3. ถ้า y = f(x) = xn เมื่อ n เป็นจำนวนจริง dy/dx = f/(x) =nxn-1
สูตรที่ 4. ถ้า y = f(x) = g(x) + h(x) dy/dx = g/ (x) + h/ (x)
สูตรที่ 5. ถ้า y = f(x) = g(x) - h(x) dy/dx = g/ (x) - h/ (x)
สูตรที่ 6. ถ้า y = f(x) = cg(x) dy/dx = cg/ (x)
สูตรที่ 7. ถ้า y = f(x) = g(x) h(x) dy/dx = g/(x)h(x)+h/ (x)g(x)
สูตรที่ 8. ถ้า y = f(x) = g(x) เมื่อ h(x)  0
h(x)
dy/dx = g/(x)h(x) - h/(x)g(x)
h(x) 2
สูตรที่ 9. ถ้า y = f(x) = un เมื่อ u เป็นฟังก์ชันของ x และ n เป็นจำนวนจริงจะได้ว่า dy/dx = nun-1 du/dx

ตัวอย่าง ถ้า f(x) = (x2 + 3x + 5)8 จงหาค่าของ dy/dx
วิธีทำ dy/dx = 8(x2 + 3x + 5)7 d (x2 + 3x + 5)
dx
= 8(x2 + 3x + 5)7(2x+3)
5. วิธีหาค่าจุดสูงสุดสัมพัทธ์หรือจุดต่ำสุดสัมพัทธ์
5.1 หา dy/dx = f/(x)
5.2 ให้ dy/dx = f/(x) = 0
5.3 แก้สมการหาค่าตัวแปร x ที่จะทำให้ f(x) มีค่าสูงสุดสัมพัทธ์หรือจุดต่ำสุดสัมพัทธ์ หรือไม่เกิดค่า 2 อย่างดังกล่าวก็ได้ เราเรียกค่า x นี้ว่า ค่าวิกฤต
5.4 นำค่า x ดังกล่าวนี้มาตรวจสอบว่าทำให้ f(x) มีค่าสูงสุด หรือต่ำสุดสัมพัทธ์ หรือไม่เป็นทั้งสองอย่าง ซึ่งมีวิธีการตรวจสอบได้ 2 วิธีดังนี้
(1) ตรวจสอบดูจากเครื่องหมายความชัน
ก. ถ้าความชัน f/(x) เปลี่ยนจากบวกเป็นลบ แสดงว่าจุดดังกล่าวเป็นจุดสูงสุดสัมพัทธ์
ข. ถ้าความชัน f/(x) เปลี่ยนจากลบเป็นบวก แสดงว่าจุดดังกล่าวเป็นจุดต่ำสุดสัมพัทธ์
ค. ถ้าไม่เป็นไปตามข้อ ก หรือ ข แสดงว่าจุดดังกล่าวไม่เป็นทั้งจุดสูงสุดและต่ำสุดสัมพัทธ์
(2) ตรวจสอบดูจากเครื่องหมายของ f//(x)
ก. ถ้า f//(x) > 0 แสดงว่าเป็นจุดต่ำสุดสัมพัทธ์
ข. ถ้า f//(x) < 0 แสดงว่าเป็นจุดสูงสุดสัมพัทธ์
ค. ถ้า f//(x) = 0 แสดงว่าการตรวจสอบวิธีนี้ใช้ไม่ได้ ต้องย้อนกลับไปใช้วิธี(1)

ตัวอย่างมันส์ๆจงหาอนุพันธ์ของฟังก์ชัน  

เริ่มต้นความมันส์ เราใช้นิยามมาอ้างอิงกันเลย เพราะว่าอนุพันธ์ คือการหา  
ดังนั้นเราเลยจะได้ว่าสำหรับฟังก์ชันนี้ อนุพันธ์คือ 
ถึงขั้นตอนนี้ก็ใช้ความรู้เรื่องลิมิตกันหน่อย เพราะว่ามันอยู่ในรูป Indeterminate Form (แล้วจะคุยกันอีกทีนะครับ)
= 
= 
= 
= 
= 

เริ่มต้น เราทราบว่า อัตราการเปลี่ยนแปลงเฉลี่ย หาได้จากการเปลี่ยนแปลงของสิ่งสุดท้ายเทียบกับสิ่งเริ่มต้น ที่เห็นกันบ่อยๆ ก็คืออัตราการเปลี่ยนแปลงของระยะทางเทียบกับเวลา



เอาตัวอย่างที่พูดไว้แรกสุด สมมติเนยสดขับรถจากบ้านไปที่เที่ยวของเนยสด ออกเดินทางเวลา 8 โมงตรง ถึงที่หมาย 9 โมงตรง จากจุดเริ่มต้นที่บ้านซึ่งห่างจากประตูท่าแพ 10 กิโลเมตร ไปยังที่เที่ยวของเขาซึ่งห่างจากประตูท่าแพ 30 กิโลเมตร (เอาเวอร์ๆนิดนึง)

ดังนั้น อัตราการเปลี่ยนแปลงของระยะทางกับเวลาเฉลี่ย ก็หาได้จาก  เท่ากับ 20 กิโลเมตรต่อชั่วโมงนั่นเอง



ต่อมาเราสนใจที่จะหาการเปลี่ยนแปลง ณ ขณะหนึ่งขณะใดเทียบกับเวลา ในการนี้เราต้องฟังก์ชันขึ้นมา สำหรับการเปลี่ยนแปลง h ใด ๆ นั่นคือ สร้าง  ซึ่งเท่ากับ f'(x) (ในที่นี้ ไม่ระบุฟังก์ชันไว้นะครับ) นั่นหมายความว่า การเคลื่อนที่ของเนยสดนั้นจะถูกกำหนดโดยฟังก์ชันใด ๆ ที่ระบุไว้



ทีนี้ถ้าเกิดว่าเราสนใจตอนที่เนยสดเดินทางได้ระยะทางน้อยมากๆๆๆๆ ที่จุดใดจุดหนึ่ง (สมมติให้จุดนั้นคือ a ก็คือเราก็จัดการใส่ลิมิตให้กับการเปลี่ยนปลง แล้วแทนค่าที่เราต้องการ นั่นคือ เราก็ทำการหา f'(x) โดยที่ x = a ก็คือหาค่า f'(x) = a



สรุปง่าย ๆ ก็คือ

- อัตราการเปลี่ยนแปลงเฉลี่ย คือ 

- อัตราการเปลี่ยนแปลงขณะหนึ่งของ f เทียบกับ x คือ 

- อัตราการเปลี่ยนแปลงขณะหนึ่งของ f เทียบกับ x ที่ x = a คือ การหา f'(a) นั่นเอง

แหล่งที่มา  http://www.vcharkarn.com/vblog/34367/1

http://www.vcharkarn.com/vblog/34367/2

นางสาวสุวิภา พันธุมิตร ม.6/2 เลขที่ 20

ทฤษฎีบทมูลฐานของแคลคูลัส เบื้องต้น

ทฤษฎีบทมูลฐานของแคลคูลัสกล่าวว่า การหาอนุพันธ์และ
การหาปริพันธ์เป็นวิธีการที่ตรงกันข้ามกัน กล่าวคือ
ถ้าเราสร้างฟังก์ชันที่เป็นปริพันธ์ของฟังก์ชันหนึ่งขี้นมา
อนุพันธ์ของฟังก์ชันที่เราสร้าง ก็จะเท่ากับฟังก์ชันนั้น นอกจากนี้
เรายังหาปริพันธ์จำกัดเขตได้ด้วยการกำหนดค่าให้กับปฏิยานุพันธ์

ทฤษฎีบทมูลฐานของแคลคูลัสเขียนในรูปสัญลักษณ์คณิตศาสตร์ได้ดังนี้: ถ้า f เป็นฟังก์ชันที่มีความต่อเนื่องบนช่วง [a, b] และ F เป็นปฏิยานุพันธ์ของ f บนช่วง [a, b] แล้ว

และสำหรับทุก x ในช่วง [a, b] จะได้ว่า

ความจริงข้อนี้ปรากฏแก่ทั้งนิวตัน และไลบ์นิซ
ซึ่งเป็นกุญแจนำไปสู่
การขยายผลลัพธ์เชิงวิเคราะห์อย่างมากมายหลังจากงานของทั้งสองเป็นที่รู้จัก.
ความเชื่อมโยงนี้
ทำให้เราสามารถย้อนความเปลี่ยนแปลงทั้งหมดในฟังก์ชันในช่วงหนึ่ง
จากอัตราการเปลี่ยนแปลงในขณะใดขณะหนึ่ง โดยการหาปริพันธ์ของส่วนหลัง.
ทฤษฎีบทมูลฐานนี้ยังให้วิธีในการคำนวณหา ปริพันธ์จำกัดเขต
ด้วยวิธีทางพีชคณิตเป็นจำนวนมาก โดยไม่ต้องใช้วิธีการหาลิมิต ด้วยการหาปฏิยานุพันธ์. ทฤษฎีบทนี้ยังอนุญาตให้เราแก้สมการเชิงอนุพันธ์ ซึ่งคือสมการที่เกี่ยวข้องกันระหว่าง ฟังก์ชันที่ไม่ทราบค่า และอนุพันธ์ของมัน. สมการเชิงอนุพันธ์นั้นมีอยู่ทั่วไปในวิทยาศาสตร์

แหล่งที่มา  http://th.wikipedia.org/wiki/%E0%B9%81%E0%B8%84%E0%B8%A5%E0%B8%84%E0%B8%... และ  http://www.tewlek.com/anet_cal.html

  
ชื่อ นายนัฐพงษ์ อินทวารี  ชั้นมัธยมศีกษาปีที่ 6/2  เลขที่ 4

อนุพันธ์ :: ว่าด้วยลิมิต

แคลคูลัสเป็นวิชาอเนกประสงค์ เอาไปใช้กับอะไรก็ได้
ไม่เฉพาะหาอัตราเร็วหรืออัตราการเจริญเติบโต
การคำนวณทางแคลคูลัสต้องการวัตถุดิบที่เป็น “ฟังก์ชันต่อเนื่อง”
แปลว่าเป็นปริมาณอะไรก็ตามที่มีการเปลี่ยนแปลง
และเป็นการเปลี่ยนแปลงแบบค่อยเป็นค่อยไป มีความต่อเนื่อง
ไม่กระโดดเป็นขั้นๆ สามารถนำมาคำนวณเพื่อหาอัตราการเปลี่ยนแปลง ณ
จุดจุดหนึ่งได้ทั้งนั้น

จากความหมายทางเรขาคณิต เรานิยามอนุพันธ์ว่าเป็น “ลิมิต”
ของความชันกราฟรอบๆจุดจุดหนึ่ง สมมุติว่าต้องการหาอนุพันธ์ของฟังก์ชัน f
ที่จุด x เราจะสร้างสูตรของอนุพันธ์โดยใช้ความชันกราฟดังนี้

จุดที่อยู่รอบๆจุด x หาได้โดยขยับไปข้างๆ x เป็นระยะ h ซึ่งมีค่าน้อยๆทางซ้ายหรือทางขวาก็ได้ จะได้จุดใหม่คือ x+h

ค่าของฟังก์ชันที่ตำแหน่ง x คือ f(x) และค่าของฟังก์ชันที่เปลี่ยนไปเมื่อเลื่อนจุดคือ f(x+h)

อัตราการเปลี่ยนแปลงเฉลี่ยหาได้จากความชันของเส้นตรงที่ผ่านจุด (x, f(x)), และ (x+h, f(x+h))

อัตราการเปลี่ยนแปลง (เฉลี่ย) =

อนุพันธ์ที่จุด x (เขียนว่า f’(x) หรือ เมื่อ y = f(x)) หาได้จากอัตราการเปลี่ยนแปลงที่ว่านี้เมื่อบีบให้ h แคบลงๆเรื่อยๆจนกลายเป็น 0 จะได้ว่า

ค่าของ f’(x) ก็จะเป็นความชันกราฟของฟังก์ชัน f ที่จุด x
จุดเดียว ไม่ใช่ความชันเฉลี่ยอีกต่อไป เพราะจุด x กับ x+h
นั้นเลื่อนมาอยู่ติดกันแล้ว
ถ้ามีฟังก์ชันความสูงของต้นไม้เมื่อเทียบกับเวลามาให้
เราก็สามารถหาได้ว่าตอนเที่ยงวันที่ 3 พอดีเป๊ะ
ต้นไม้มีอัตราการเจริญเติบโตเท่าไหร่

ที่มาของข้อมูล  http://fltsolver.wordpress.com/2011/11/15/%E0%B9%81%E0%B8%84%E0%B8%A5%E0...

 นางสาว รัตนากร  ธรรมนิยม ม.6/2 เลขที่14

 แคลคูลัส เป็นสาขาหลักของคณิตศาสตร์ซึ่งพัฒนามาจากพีชคณิต เรขาคณิต และปัญหาทางฟิสิกส์ แคลคูลัสมีต้นกำเนิดจากสองแนวคิดหลัก ดังนี้

แนวคิดแรกคือ แคลคูลัสเชิงอนุพันธ์ (Differential Calculus) เป็นทฤษฎีที่ว่าด้วยอัตราการเปลี่ยนแปลง และเกี่ยวข้องกับการหาอนุพันธ์ของฟังก์ชันทางคณิตศาสตร์ ตัวอย่างเช่น การหา ความเร็ว, ความเร่ง หรือความชันของเส้นโค้ง บนจุดที่กำหนดให้. ทฤษฎีของอนุพันธ์หลายส่วนได้แรงบันดาลใจจากปัญหาทางฟิสิกส์

แนวคิดที่สองคือ แคลคูลัสเชิงปริพันธ์ (Integral Calculus) เป็นทฤษฎีที่ได้แรงบันดาลใจจากการคำนวณหาพื้นที่หรือปริมาตรของรูปทรงทางเรขาคณิตต่าง ๆ. ทฤษฎีนี้ใช้กราฟของฟังก์ชันแทนรูปทรงทางเรขาคณิต และใช้ทฤษฎีปริพันธ์ (หรืออินทิเกรต) เป็นหลักในการคำนวณหาพื้นที่และปริมาตร

ทั้งสองแนวคิดที่กำเนิดจากปัญหาที่ต่างกันกลับมีความสัมพันธ์กันลึกซึ้ง โดยทฤษฎีบทมูลฐานของแคลคูลัสกล่าวว่า แท้จริงแล้วทฤษฎีทั้งสองเปรียบเสมือนเป็นด้านทั้งสองของเหรียญอันเดียวกัน นั่นคือเป็นสิ่งเดียวกันเพียงแต่มองคนละมุมเท่านั้น (โดยคร่าว ๆ เรากล่าวได้ว่าอนุพันธ์และปริพันธ์เป็นฟังก์ชันผกผันของกันและกัน). ในการสอนแคลคูลัสเพื่อความเข้าใจตัวทฤษฎีอย่างลึกซึ้ง ควรกล่าวถึงทั้งสองทฤษฎีและความสัมพันธ์นี้ก่อน แต่การศึกษาในปัจจุบันมักจะกล่าวถึงแคลคูลัสเชิงอนุพันธ์ก่อนเพียงอย่างเดียว เนื่องจากนำไปใช้งานได้ง่ายกว่า

http://th.wikipedia.org/wiki/%E0%B9%81%E0%B8%84%E0%B8%A5%E0%B8%84%E0%B8%B9%E0%B8%A5%E0%B8%B1%E0%B8%AA

ชื่อ  นางสาว นุชนาถ บุญเกิด ชั้นมัธยมศึกษาปีที่ 6/2  เลขที่  18

แคลคูลัส เป็นสาขาหลักของคณิตศาสตร์ซึ่งพัฒนามาจากพีชคณิต เรขาคณิต และปัญหาทางฟิสิกส์ แคลคูลัสมีต้นกำเนิดจากสองแนวคิดหลัก ดังนี้

แนวคิดแรกคือ แคลคูลัสเชิงอนุพันธ์ (Differential Calculus) เป็นทฤษฎีที่ว่าด้วยอัตราการเปลี่ยนแปลง และเกี่ยวข้องกับการหาอนุพันธ์ของฟังก์ชันทางคณิตศาสตร์ ตัวอย่างเช่น การหา ความเร็ว, ความเร่ง หรือความชันของเส้นโค้ง บนจุดที่กำหนดให้. ทฤษฎีของอนุพันธ์หลายส่วนได้แรงบันดาลใจจากปัญหาทางฟิสิกส์

แนวคิดที่สองคือ แคลคูลัสเชิงปริพันธ์ (Integral Calculus) เป็นทฤษฎีที่ได้แรงบันดาลใจจากการคำนวณหาพื้นที่หรือปริมาตรของรูปทรงทางเรขาคณิตต่าง ๆ. ทฤษฎีนี้ใช้กราฟของฟังก์ชันแทนรูปทรงทางเรขาคณิต และใช้ทฤษฎีปริพันธ์ (หรืออินทิเกรต) เป็นหลักในการคำนวณหาพื้นที่และปริมาตร

ทั้งสองแนวคิดที่กำเนิดจากปัญหาที่ต่างกันกลับมีความสัมพันธ์กันลึกซึ้ง โดยทฤษฎีบทมูลฐานของแคลคูลัสกล่าวว่า แท้จริงแล้วทฤษฎีทั้งสองเปรียบเสมือนเป็นด้านทั้งสองของเหรียญอันเดียวกัน นั่นคือเป็นสิ่งเดียวกันเพียงแต่มองคนละมุมเท่านั้น (โดยคร่าว ๆ เรากล่าวได้ว่าอนุพันธ์และปริพันธ์เป็นฟังก์ชันผกผันของกันและกัน). ในการสอนแคลคูลัสเพื่อความเข้าใจตัวทฤษฎีอย่างลึกซึ้ง ควรกล่าวถึงทั้งสองทฤษฎีและความสัมพันธ์นี้ก่อน แต่การศึกษาในปัจจุบันมักจะกล่าวถึงแคลคูลัสเชิงอนุพันธ์ก่อนเพียงอย่างเดียว เนื่องจากนำไปใช้งานได้ง่ายกว่า

 http://th.wikipedia.org/wiki/%E0%B9%81%E0%B8%84%E0%B8%A5%E0%B8%84%E0%B8%B9%E0%B8%A5%E0%B8%B1%E0%B8%AA

นางสาวภาวิณี  พลท้าว เลขที่ 25 ชั้นม.6/2 โรงเรียนนนนทบุรีพิทยาคม

 คลคูลัส เป็นสาขาหลักของคณิตศาสตร์ซึ่งพัฒนามาจากพีชคณิต เรขาคณิต และปัญหาทางฟิสิกส์ แคลคูลัสมีต้นกำเนิดจากสองแนวคิดหลัก ดังนี้

แนวคิดแรกคือ แคลคูลัสเชิงอนุพันธ์ (Differential Calculus) เป็นทฤษฎีที่ว่าด้วยอัตราการเปลี่ยนแปลง และเกี่ยวข้องกับการหาอนุพันธ์ของฟังก์ชันทางคณิตศาสตร์ ตัวอย่างเช่น การหา ความเร็ว, ความเร่ง หรือความชันของเส้นโค้ง บนจุดที่กำหนดให้. ทฤษฎีของอนุพันธ์หลายส่วนได้แรงบันดาลใจจากปัญหาทางฟิสิกส์

แนวคิดที่สองคือ แคลคูลัสเชิงปริพันธ์ (Integral Calculus) เป็นทฤษฎีที่ได้แรงบันดาลใจจากการคำนวณหาพื้นที่หรือปริมาตรของรูปทรงทางเรขาคณิตต่าง ๆ. ทฤษฎีนี้ใช้กราฟของฟังก์ชันแทนรูปทรงทางเรขาคณิต และใช้ทฤษฎีปริพันธ์ (หรืออินทิเกรต) เป็นหลักในการคำนวณหาพื้นที่และปริมาตร

ทั้งสองแนวคิดที่กำเนิดจากปัญหาที่ต่างกันกลับมีความสัมพันธ์กันลึกซึ้ง โดยทฤษฎีบทมูลฐานของแคลคูลัสกล่าวว่า แท้จริงแล้วทฤษฎีทั้งสองเปรียบเสมือนเป็นด้านทั้งสองของเหรียญอันเดียวกัน นั่นคือเป็นสิ่งเดียวกันเพียงแต่มองคนละมุมเท่านั้น (โดยคร่าว ๆ เรากล่าวได้ว่าอนุพันธ์และปริพันธ์เป็นฟังก์ชันผกผันของกันและกัน). ในการสอนแคลคูลัสเพื่อความเข้าใจตัวทฤษฎีอย่างลึกซึ้ง ควรกล่าวถึงทั้งสองทฤษฎีและความสัมพันธ์นี้ก่อน แต่การศึกษาในปัจจุบันมักจะกล่าวถึงแคลคูลัสเชิงอนุพันธ์ก่อนเพียงอย่างเดียว เนื่องจากนำไปใช้งานได้ง่ายกว่า

อนึ่ง การศึกษาแคลคูลัสอย่างละเอียดในเวลาต่อมา ได้ทำให้เกิดศาสตร์ใหม่ ๆ ทางคณิตศาสตร์มากมาย เช่น คณิตวิเคราะห์ และ ทฤษฎีการวัด เป็นต้น

 http://th.wikipedia.org/wiki/%E0%B9%81%E0%B8%84%E0%B8%A5%E0%B8%84%E0%B8%B9%E0%B8%A5%E0%B8%B1%E0%B8%AA